Sphere Carving: Bounding Volumes for Signed Distance Fields

Teaser image — Given an input black box conservative signed distance field, we automatically generate a tight bounding volume around the implicitly defined object, agnostic of its representation. Starting from a large initial volume around the object, we iteratively carve the space using spheres defined by the signed distance field. The bounding volume is then constructed as an assembly of convex primitives (half-spaces, ellipsoids) and allows for faster field function queries.

Abstract

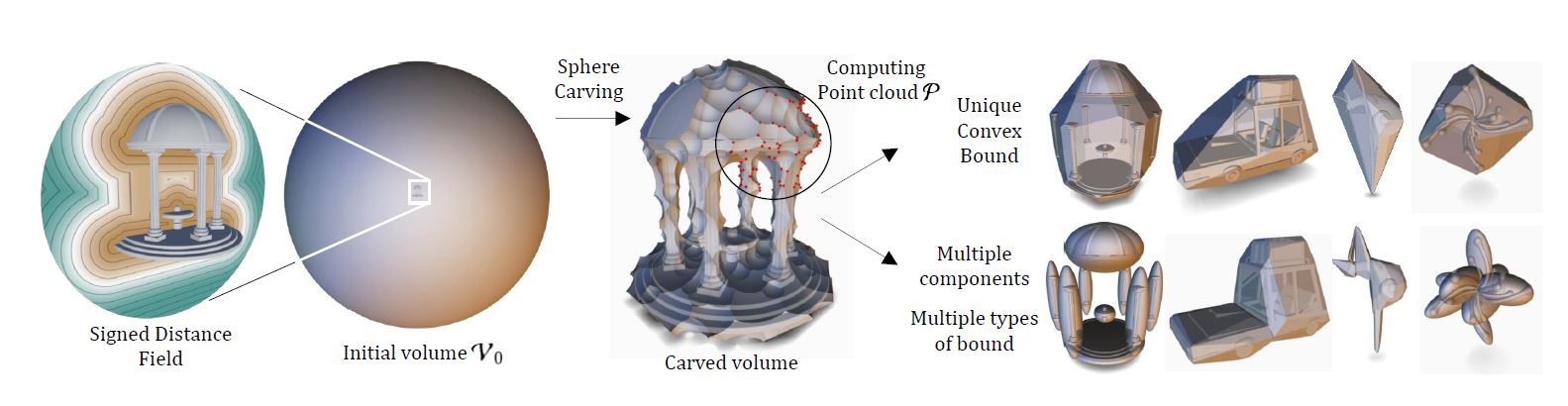
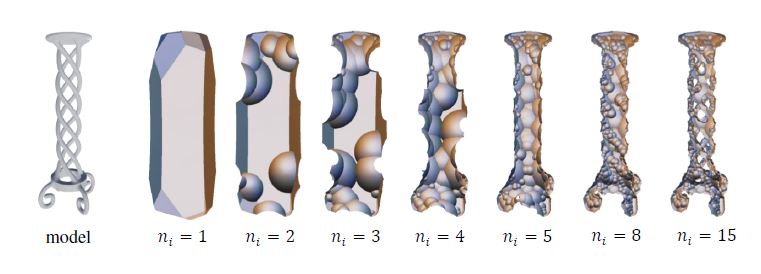
We introduce Sphere Carving, a novel method for automatically computing bounding volumes that closely bound a procedurally defined implicit surface. Starting from an initial bounding volume located far from the object, we iteratively approach the surface by leveraging the signed distance function information. Field function queries define a set of empty spheres, from which we extract intersection points that are used to compute a bounding volume. Our method is agnostic of the function representation and only requires a conservative signed distance field as input. This encompasses a large set of procedurally defined implicit surface models such as exact or Lipschitz functions, BlobTrees, or even neural representations. Sphere Carving is conceptually simple, independent of the function representation, requires a small number of function queries to create bounding volumes, and accelerates queries in Sphere Tracing and polygonization.

Workflow

Input — Visualization of the spheres carving the initial volume through several iteration of Sphere Carving. The carved volume converges to the model even for complex geometric shapes with a non-zero genus and several components.

Pipeline — Given a conservative signed distance function f and a volume $V_{0}$ , Sphere Carving progressively carves spheres $S$ around the object while maintaining a point set $P$ defined as the trilateration of $S$ . Next, we construct bounding volumes fitting the object using an approximate convex decomposition algorithm over $P$ . The resulting set of convex shapes is then used to define an accelerated function $\tilde{f}$ .

Results — Bounding volumes obtained by Sphere Carving on a variety of quasi-exact and conservative signed distance field.

Citation

@article{schott2025, title = {Sphere Carving: Bounding Volumes For Signed Distance Fields}, author = {Schott, Hugo and Thonat, Theo and Lambert, Thibaud and Guérin, Eric and Galin, Eric and Paris, Axel}, journal = {ACM Transaction on Graphics (SIGGRAPH '25 Conference Proceedings)}, publisher = {ACM}, year = {2025}, number = {}, volume = {} }